An Orbital Siphon
Synopsis
Orbital towers (also called skyhooks or beanstalks) have been
discussed by a number of scientists and authors
(e.g. J. Pearson and A.C.Clarke) over the past 30 years.
This web page uses a simple Java physical simulation model to
demonstrate free orbital motion, tethered satellites, and several
equatorially-sited orbital towers. But it is mainly intended to demonstrate the
possibility of a variant orbital tower - the siphon - which uses the
centrifugal force generated in a high rigid tower to raise a 250,000 km
train of tethered vehicles. As vehicles are released from the top of
this tower, new vehicles are fed in at the base, so that the siphon
can pump vehicles continuously into space. Apart from the energy required
to build the tower and to prime it with a train of connected bodies,
the energy source for the siphon is the rotational energy of the earth:
no other power source is required.
Methodology
A simple physical simulation model is developed.
The model calculates accelerations in x,y dimensions
due to gravitational forces and tension forces in connecting cables.
Bodies are regarded as point masses, and
connecting cables are regarded as massless.
The calculated accelerations of each body allow the (x,y)
location after a short interval of time to be found.
The simulation model only uses (x,y) dimensions
in a planetary equatorial
plane, and it does not include the effect of other bodies (e.g. moons).
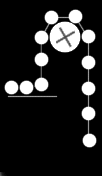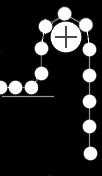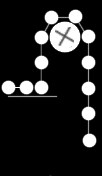 The proposed orbital siphon differs from 'conventional' orbital
towers by being rigid. This is necessary to maintain the angular
velocity of material rising up the tower: the siphon is subject to
bending forces. Conventional towers, even those greater than 150,000
km in radius, are not subject to any bending forces.
For all bodies below geostationary,
gravitational forces exceed centrifugal forces, and they tend to fall.
For all bodies above geostationary, centrifugal
forces exceed gravitational forces, and they tend to rise.
The principle of the siphon is that, in a connected chain of bodies,
if enough of the mass is above geostationary, the net tendency of
the tower is to rise.
Although the analogy is inexact, it is as if the geostationary point was
the wheel of a pulley with two sets of weights hanging off either side.
Where the weights of both exactly counterbalance each other, the
system remains motionless. But if one side weighs more than the other,
it descends, pulling up the weight on the other side.
In the orbital siphon, the pull of one side is gravitation,
and on the other side centrifugal force,
and the excess of centrifugal force causes a net outward
motion of the set of connected bodies.
The proposed orbital siphon differs from 'conventional' orbital
towers by being rigid. This is necessary to maintain the angular
velocity of material rising up the tower: the siphon is subject to
bending forces. Conventional towers, even those greater than 150,000
km in radius, are not subject to any bending forces.
For all bodies below geostationary,
gravitational forces exceed centrifugal forces, and they tend to fall.
For all bodies above geostationary, centrifugal
forces exceed gravitational forces, and they tend to rise.
The principle of the siphon is that, in a connected chain of bodies,
if enough of the mass is above geostationary, the net tendency of
the tower is to rise.
Although the analogy is inexact, it is as if the geostationary point was
the wheel of a pulley with two sets of weights hanging off either side.
Where the weights of both exactly counterbalance each other, the
system remains motionless. But if one side weighs more than the other,
it descends, pulling up the weight on the other side.
In the orbital siphon, the pull of one side is gravitation,
and on the other side centrifugal force,
and the excess of centrifugal force causes a net outward
motion of the set of connected bodies.
The Simulation Model
The simulation model is developed in stages from a simple
gravitational model, through a variety of orbital towers, to
the rigid tower siphon. Only one applet is used, with different
parameters for each stage.
The thumbnails show the sort of image you see with each model.
The simulation models show the view down onto the planet pole.
| 1 | 
| Gravitational Model This is the essential primary model, in which bodies move under the influence of their mutual gravitational attraction. In this version, various bodies are given randomized velocities around a central immobile planet. See also Simple Orbital Model |
| 2 | 
| Elastic Model The next step is to tie the bodies together with elastic cables. This introduces another set of forces acting on the bodies in addition to gravity. The ties between bodies are shown in increasing blue to the extent that they are stretched, and in increasing red as they are compressed. In this version, some bodies are tied together in chains, randomly, and each body given randomized initial velocities. |
| 3 | 
| Tethered Satellite Model The next stage is to tie a single body to the surface of the rotating planet. Even though the body is further away from the planet than the geostationary distance of 42,000 km, the effect of the tie is to constrain the body to geosynchronous orbit. |
| 4 | 
| Short Tower Collapse A tower can be thought of as a chain of connected bodies tied to the equator of the rotating planet. Does it stay up? Not always. In this version, the tower is too short, and gravitational forces exceed centrifugal forces: it collapses, and during its collapse ties break, resulting in part of the tower spinning out into space. |
| 5 | 
| Pearson's Tower It can be shown that a tower must be at least 150,000 km in radius if it is not to collapse. This is Pearson's tower. Such a tower is a satellite which does not have to connected to the planet. It is rather tricky to model, however, because such a tower represents a balance point, and if slightly too long will spin out into space, and if slightly too short will collapse. The version shown is a (poor) approximation. |
| 6 | 
| 230,000 km high tower model With a collapsing short tower and a balanced tower shown, this model shows a tower greater than 150,000 km high. The tower is in tension throughout its length, with a maximum at geostationary distance. If released at the base, it spins out into space. |
| 7 | 
| Optimized high tower model Simply creating a string of beads with bodies set at equal distances along its length results in oscillations in the tower because the tensile and gravitational forces acting on each body are not equalized. In the optimized version, bodies are initialized at distances along the string such that these forces are equalized. This minimizes radial oscillations, and the bodies move in near-perfect circles. |
| 8 | 
| Base feed high tower collapse Since a high tower (radius 230,000 km) is in tension, and needs to be held down by some massive weight, it can be seen that the tendency of such towers is to move outwards. In this model, the base is released, and new bodies and ties are added at the base as the tower rises. As can be seen, this only works for a while, and after rising, the tower falls back. |
| 9 | 
| Free Body Rigid Tower The failure of the last model happened because, as the tower rose, the angular velocity of each body (with respect to the planet) fell. Fairly rapidly, the outer parts were moving too slowly. In this model, a constant angular velocity is maintained by constraining the chain of rising bodies within a 250,000 km rigid tower. There are no ties, and bodies are allowed to move freely within the rigid tower. Some fall, and others accelerate into space |
| 10 | 
| Base Feed Rigid Tower In this model, a rigid tower contains a chain of linked bodies which are allowed to accelerate out into space, while new bodies and ties are added at the base. Bodies fly out faster and faster until the stresses in the chain result in ties snapping. |
| 11 | 
| Restricted Base Feed Rigid Tower - Siphon In an attempt to prevent the chain accelerating faster and faster up the rigid tower, the lowest body is restrained to an arbitrary maximum velocity. Rather than being freely fed out, the tower is fed out slowly. As bodies reach the top of the rigid tower, their ties are released, and they fly out into space. This siphon steadily feeds bodies out. It takes some 34 hours for a body to ascend from the planet surface to the top of the rigid tower. |
| 12 | 
| Increasing body mass Siphon All the towers shown so far are made up of bodies of equal mass. In this example, the bodies fed in at the base are always a small percentage more massive than their predecessors. The net mass of bodies in the tower rises. This shows that a siphon can be used to raise an increasing flow of material. |
| 13 | 
| One shot per revolution Siphon The two siphons shown so far spray bodies indiscriminately in all directions. In this variant model, bodies which reach the top of the rigid tower are not untied, but are held in a 'tail' extending from its top, and this tail is released once per revolution in a particular direction. |
Comments and Conclusions
The conclusion drawn from this simple theoretical model is that a siphon
appears to be a physical possibility. The engineering problems are not addressed.
Such siphons offer the possibility of launching hundreds or even thousands of tons
of material into space daily at velocities that can exceed
escape velocity from the sun ( 42 km/s ).
Orbital towers such as Pearson's or Arthur C. Clarke's require no lateral
strength. A working siphon, however, is subject to lateral forces that act against
its direction of motion - it tends to bend backwards.
An extension of this idea is to have one tower as an ascent tower, and
the other as a descent tower, and loop a cable car system around the two.
The principal objection to orbital towers is that the costs of putting
so much material into orbit is prohibitive - Jerome Pearson estimated in
1974 that some 25,000 rocket launches would be required to build his tower.
But the siphon offers the outline of a solution to this problem: once a
minimum tower - perhaps a Fullerene thread - was deployed, it could be used
to haul up a larger tower, in a bootstrap operation, where most of the
energy would be expended in bringing materials to the tower base.
References
Jerome Pearson - The orbital tower: a spacecraft launcher using the
Earth's rotational energy. Acta Astronautica 1974 Vol.2 pp 785-799
Arthur C. Clarke - The Space Elevator: Thought Experiment or Key to the
Universe? Pergamon Press 1981 http://plains.uwyo.edu/~mickray/clark.htm Arthur C. Clarke. The Fountains of Paradise. Pan.
Implications of Molecular Nanotechnology. T.L.McKendree.
http://www.xerox.com/nanotech/nano4/mckendreePaper.html
Further siphon simulation pages
Origins of the Siphon: the Coal Planet
 How is such a tower to be kept rigid? One possible
answer is that the siphon is made up of 2 orbital towers, connected by
struts, and aligned E-W. As material travels up the trailing Western tower,
it deflects westwards, and in so doing stretches the leading Eastern tower.
The two towers act as the top and bottom rails of a beam subject to uniform
bending along its length.
How is such a tower to be kept rigid? One possible
answer is that the siphon is made up of 2 orbital towers, connected by
struts, and aligned E-W. As material travels up the trailing Western tower,
it deflects westwards, and in so doing stretches the leading Eastern tower.
The two towers act as the top and bottom rails of a beam subject to uniform
bending along its length.
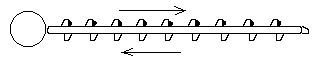 The advantage of this would be that the lateral forces generated by the
ascending cable cars would be largely counteracted by the opposite lateral
forces generated by the descending tower, at least if payloads were small in
mass relative to the cable cars. Such a system would remain principally a
way of putting material into space, rather than collecting it from space,
because if the mass of material in the descent tower approached that of the
ascent tower, the system would cease operating.
The advantage of this would be that the lateral forces generated by the
ascending cable cars would be largely counteracted by the opposite lateral
forces generated by the descending tower, at least if payloads were small in
mass relative to the cable cars. Such a system would remain principally a
way of putting material into space, rather than collecting it from space,
because if the mass of material in the descent tower approached that of the
ascent tower, the system would cease operating.
Siphon model Java class files available in Siphon.zip
Siphon model Java source code.

